Final answer:
The vertex of the parabola with the equation
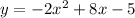 is found by using the formula x = -b/(2a). The vertex coordinates are (2, -5).
is found by using the formula x = -b/(2a). The vertex coordinates are (2, -5).
Step-by-step explanation:
To find the vertex of the parabola with the equation
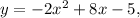 we need to use the vertex form of a quadratic equation, which is
we need to use the vertex form of a quadratic equation, which is
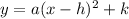 , where (h, k) is the vertex of the parabola. For the given equation, a = -2. The x-coordinate of the vertex can be found using the formula x = -b/(2a), where a and b are coefficients from the quadratic equation y = ax2 + bx + c.
, where (h, k) is the vertex of the parabola. For the given equation, a = -2. The x-coordinate of the vertex can be found using the formula x = -b/(2a), where a and b are coefficients from the quadratic equation y = ax2 + bx + c.
Here's a step-by-step method to find the vertex:
Identify the coefficients: a = -2, b = 8.
Use the formula x = -b/(2a) to find the x-coordinate of the vertex: x = -8/(2*(-2)) = 2.
Plug this x-value into the original equation to find the y-coordinate: y = -2(2)2 + 8*2 - 5 = -16 + 16 - 5 = -5.
Therefore, the vertex of the parabola is (2, -5).