Question

Formulate the quadratic function that contains the points (-1,4), (0,2) and (2,4).

f(x) = x2 + x + 2
f(x) = x2 + x - 2
f(x) = x2 - x + 2
f(x) = x2 - x - 2

Answer 1

`f(x)=x^2-x+2`

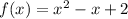
Explanation:

Quadratic equation form :
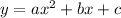`y=ax^2+bx+c` --1

We are given points :(-1,4), (0,2) and (2,4).

Substitute the point (0,2) in the quadratic equation.

`2=a(0)^2+b(0)+c`

`2=c`

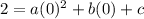
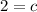
Thus the value of c is 2

Substitute the value of c in 1

Thus equation becomes:
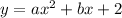`y=ax^2+bx+2` --2

Now substitute the point (-1,4) in 2

`4=a(-1)^2+b(-1)+2`

`4=a-b+2`

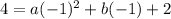
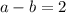`a-b=2` ---3

Now substitute point (2,4) in 2

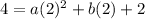
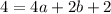
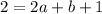
`4=a(2)^2+b(2)+2`

`4=4a+2b+2`

`2=2a+b+1`

`2a+b=1` --4

Now solve 3 and 4 to find the value of a and b

Substitute the value of a from 3 in 4

`2(2+b)+b=1`

`4+2b+b=1`

`4+3b=1`

`3b=-3`

`b=-1`

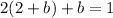
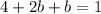
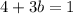
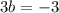
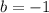
Substitute the value of b in 3

`a-(-1)=2`

`a+1=2`

`a=2-1`

`a=1`

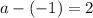
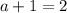
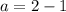
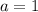
Thus a = 1, b =-1 and c = 2

Substitute the values in 1

`y=x^2-x+2`

Thus the quadratic function that contains the points (-1,4), (0,2) and (2,4) is
`f(x)=y=x^2-x+2`

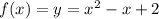
Hence Option 3 is correct.

Answer 2

f(x) = x2 - x + 2

f(-1)=(-1)²-(-1)+2=4 contain the point (-1,4)

f(0) = 0²-0+2 = 2 contain the point (0,2)

f(2) = 2²-2+2 =4 contain the point (2,4)