Answer:
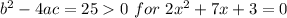
This shows the roots of the equation 2x² + 7x + 3 = 0 are distinct real roots .
Explanation:
As given the expression is given in the question .
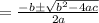
Thus the part shows the equation is factoring is represented by
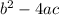 .
.
Now as the quadratic equation given is
2x² + 7x + 3 = 0
As the equation in the form ax² + bx + c = 0
a = 2 , b = 7 , c = 3
Thus put all the values in
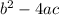
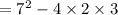
As
7² = 49
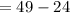
= 25
Thus
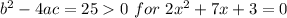
This shows the roots of the equation 2x² + 7x + 3 = 0 are distinct real roots .