ANSWER
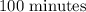
Step-by-step explanation
Let the number of minutes of calls be x.
For the first plan, the cost of the calls is $26 monthly plus an additional $0.11 for each minute of calls. This implies that the cost of calls for the first plan is:
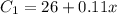
For the second plan, the cost of the calls is $22 monthly plus an additional $0.15 for each minute of calls. This implies that the cost of calls for the second plan is:
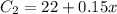
When the costs of the two plans are equal, it implies that C1 is equal to C2:
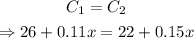
Now, we have to solve for x to find the number of minutes of calls for which the costs will be the same:
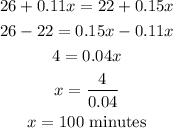
That is the answer.