Question

(DESPERATE PLEASE HURRY)
question down below
please show the work

Answer 1

`\boxed{\sf x = - 8}`

Explanation:

Given equation :

`16 = - 2x`

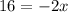
We need to find the value of x .

Solution :

`\tt \implies16 = - 2x`

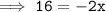
Change their sides :

`\tt \implies - 2x = 16`

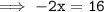
Divide both sides by -2 :-

`\tt \implies ( - 2x)/( - 2) = (16)/( - 2)`

Cancel The LHS:

• Cancel -2 and -2 :

`\tt \implies \cfrac{ \cancel{ - 2}x}{ \cancel{ - 2}} = \cfrac{16}{ 2}`

`\tt \implies \cfrac{1x}{1} = \cfrac{16}{ - 2}`

`\tt \implies{1x} = \cfrac{16}{ - 2}`

`\tt \implies{x} = \cfrac{16}{ - 2}`

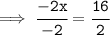
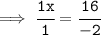
Cancel the RHS :

• Cancel 16 and -2 by 2:

`\tt \implies{x} = \cfrac{ \cancel{16} {}^( 8) }{ \cancel{ {- 2}} ^( - 1) }`

• Results to,

`\tt \implies{x} = \cfrac{ 8}{ - 1}`

`\tt \implies{x} = - 8`

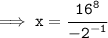
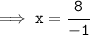
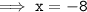
We're done!

Hence, the value of x would be -8 .

`\rule{225pt}{2pt}`

I hope this helps!

Let me know if you have any questions.