Question

Angles α and β are the two acute angles in a right triangle. Use the relationship between sine and cosine to find the value of β if β < α.sin(3x - 27) = cos(5x + 5)

A. 14
B. 15
C. 75
D. 76

Answer 1

`\boxed{\boxed{\beta=15^(\circ)}}`

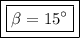
Explanation:

As given as ∠α and ∠β are the two acute angles in a right triangle.

So,

`\Rightarrow \alpha+\beta=90^(\circ)`

`\Rightarrow \alpha=90^(\circ)-\beta`

`\Rightarrow \sin \alpha=\sin(90^(\circ)-\beta)`

`\Rightarrow \sin \alpha=\cos \beta`

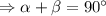
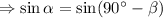
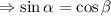
Also given as,

`\sin(3x - 27) = \cos(5x + 5)`

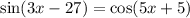
Then between (3x-27) and (5x+5), one is α and the other one is β.

And the sum of both the angles are 90°. So,

`\Rightarrow (3x - 27)+(5x + 5)=90`

`\Rightarrow 8x - 22=90`

`\Rightarrow 8x=90+22=112`

`\Rightarrow x=14`

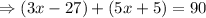
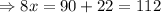
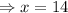
Then the measurement of the two angles are,

`3x - 27=3(14) - 27=15^(\circ)\\\\5x + 5=5(14) + 5=75^(\circ)`

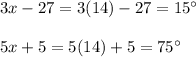
As β < α, so β=15°