Question

What is the value of the discriminant, b2 − 4ac, for the quadratic equation 0 = −2x2 − 3x + 8, and what does it mean about the number of real solutions the equation has?

The discriminant is −55, so the equation has 2 real solutions.
The discriminant is −55, so the equation has no real solutions.
The discriminant is 73, so the equation has 2 real solutions.
The discriminant is 73, so the equation has no real solutions.

Answer 1

hello:
−2x² − 3x + 8
delta = (-3)²-4(-2)(8) =9+64 = 73 ... (delta) > 0
The discriminant is 73, so the equation has 2 real solutions

Answer 2

C. The discriminant is 73, so the equation has 2 real solutions.

Explanation:

We have been given an equation
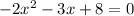`-2x^2-3x+8=0`. We are asked to determine the number of real solutions for our given equation using discriminant formula.

`D=b^2-4ac`, where,

D = Discriminant,

b = Coefficient of x or middle term.

a = Leading coefficient,

c = constant.

When
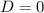`D=0`, the equation has two real and equal zeros.

When
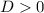`D>0`, the equation has two real and distinct zeros.

When
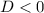`D<0`, the equation has no real zeros.

Upon substituting our given values in above formula we will get,

`D=(-3)^2-4*-2*8`

`D=9+8*8`

`D=9+64`

`D=73`

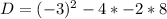
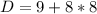
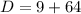
Since the value of discriminant is 73 that is greater than 0, therefore, the equation has two real zeros and option C is the correct choice.