Question

Im not sure how to solve the system?

Answer 1

`\bf \begin{cases} -24-8x=12y\\\\ 1+\cfrac{5}{9}y=-\cfrac{7}{18}x \end{cases}`

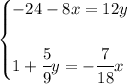
so... first off, let arrange the variables, so they align vertically

thus
`\bf \begin{cases} -8x-12y=24\\\\ \cfrac{7}{18}x+\cfrac{5}{9}y=-1 \end{cases}`

now.. let's try say.. elimination method

alrite, let's hose the "x"'s

so... we have a -8x atop and a 7/18x at the bottom, what the dickens can we multiply 7/18 so we can end up with with a positive 8? that way it becomes 8x and -8x + 8x = 0, effectively hosing the "x"s

hmm ok.. let's say... we need to multiply the 7/18 by "a".. .let's find out what "a" is then
`\bf \cfrac{7}{18}\cdot a=8\implies 7a=18\cdot 8\implies 7a=144\implies a=\cfrac{144}{7}`

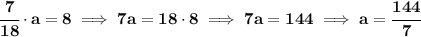
low and behold, if we multiply then, 7/18 by 144/7, we end up with "8"
so let's do that for the 2nd equation then


`\bf \begin{array}{lllrl} -8x&-12y&=&24\\\\ 8x&+\cfrac{80}{7}y&=&-\cfrac{144}{7}\\ ---&---&---&---\\ 0&-\cfrac{4}{7}y&=&\cfrac{24}{7} \end{array}\\\\ -----------------------------\\\\ \cfrac{-4y}{7}=\cfrac{24}{7}\implies -4y=\cfrac{24\cdot 7}{7}\implies -4y=24 \\\\\\ y=\cfrac{24}{-4}\implies \boxed{y=-6}`

alrite.. so..now we know y = -6, let us use that in the first equation then


`\bf -8x-12(-6)=24\implies -8x+72=24\implies -8x=24-72 \\\\\\ -8x=-48\implies x=\cfrac{-48}{-8}\implies \boxed{x=6}`