Answer: The relationship between the surface areas of the two solid figures is that the surface area of cube is 1.1 times the surface of cube.
Explanation:
Since we have given that
A sphere is inscribed in a cube.
Let the radius of sphere be 'r'.
Let the side of cube would be the diameter of sphere i.e. 2r.
So, Surface area of sphere would be

And Surface area of cube would be
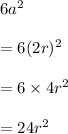
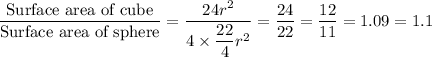
So, the relationship between the surface areas of the two solid figures is that the surface area of cube is 1.1 times the surface of cube.