Question

the spinner below shows 10 equally size slices. linda spun the dial 100 times and got the following results.A: using the results compute the experimental probability of landing on black?B: assuming that the spinner is fair compute the theoretical probability of landing on black.

Answer 1

Given:

The total number of spins =100.

`n(S)=100`

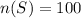
Let A be the even of landing black.

Given that the number of spins to get black =37.

`n(A)=37`

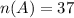
The probability of landing on black is P(A).

`P(A)=(n(A))/(n(S))`
`P(A)=(37)/(100)=0.37`

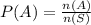
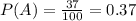
The probability of landing on black is 0.37.

B)

For the first spin.

The total number of slices in the spinner is 10.

`n(S)=10`

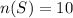
The number of black in the spinner is 3.

`n(A)=3`

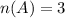
The probability of landing black is

`P(A)=(n(A))/(n(S))=(3)/(10)=0.3`

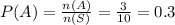
For the first spin, the probability of landing black is 0.3.

For the 10 times spin.

The sample space is 100 for 10 times spin

The number of black in favorable is 30.

The probability of landing black is

`P(A)=(n(A))/(n(S))=(30)/(100)=0.3`

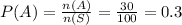
For the 100 times spin.

The sample space is 1000 for 100 times spin

The number of black in the spinner is 300.

`P(A)=(n(A))/(n(S))=(300)/(1000)=0.3`

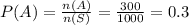
Hence the theoretical probability of landing on black is 0.3.