Answer with explanation:
Sample Size (n)=72
→P=% of people who listen to radio while they are at work =16 %
→B=1 - P= 100% - 16% =84%
→Standard Deviation when Probability and Sample Size is given
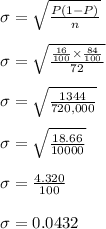
So, standard deviation of the sampling distribution of the proportion for the sample of size 72= 0.0432=0.043 (Approx)