Answer:
K= -3
Explanation:
If g(x) be the function given by
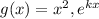
where k is a constant.
We have to find the value of k when the function has a critical point at x =

Since g'(x) =
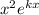
Now for critical point we will find derivative of g(x) and equate the derivative to zero.
![g'(x)=(d)/(dx)[(x^(2))(e^(kx))]](https://img.qammunity.org/2018/formulas/mathematics/high-school/s8saubjv8rffvuju4625ncm92ygwoiq7pw.png)
g'(x) =
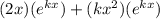
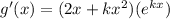
Now for
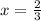
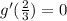
/(3)k)})=0](https://img.qammunity.org/2018/formulas/mathematics/high-school/d6qhw6nyetrubbg1jyjnpcab00rz8j8fd9.png)
Sin
 ≠ 0
≠ 0
therefore,

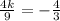
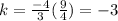
Therefore, k = -3 is the answer