Question

The volume of the pyramid shown in the figure is 9,15,21, or 63 cubic centimeters. If the slant height of the pyramid increases by 4 centimeters and its height increases by 2 centimeters, the volume of the pyramid increases by 6,9,12 or 21 cubic centimeters.

Answer 1

the answer is 15 and 6

Answer 2

`\bf \textit{volume of a pyramid}\\\\ V=\cfrac{1}{3}Bh\qquad \begin{cases} B=base\\ h=height\\ ----------\\ B=width\cdot length\\ length=3\qquad width=3\\ B=3\cdot 3=9\\ h=5 \end{cases}\\\\ -----------------------------\\\\ \textit{what if we increase the slant height by 4 and height by 2?} \\\\\\ V=\cfrac{1}{3}Bh\qquad \begin{cases} B=width\cdot length\\ length=3\qquad width=3\\ B=3\cdot 3=9\\ h=7 \end{cases}`

the slant-height plays no role on that equation to get the volume, only the height does, and the Base, so the slant-height going from 7 to 11, has no bearing on the volume, since we know the height


`\bf V=\cfrac{1}{3}\cdot 9\cdot 5\implies V=3\cdot 5\implies V=15 \\\\\\ V=\cfrac{1}{3}\cdot 9\cdot 7\implies V=3\cdot 7\implies V=21`

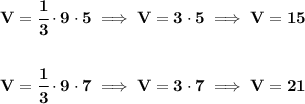
so hmmm, it was 15, then it went up to 21, 21-15 = 6, went up by 6 units