Question

the bases of the prism are equilateral triangle and its lateral faces are rectangular regions. given the length of the edge base is 6, and the altitude of the prism is 10, compute the area of the total surface of the prism

Answer 1

The total surface area of the prism is the sum of the areas of the bases and the areas of the lateral sides:

`S=2\cdot A_b+A_l`

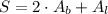
The area of the base corresponds to the area of an equilateral triangle:

`A_b=\frac{\sqrt[]{3}}{4}\cdot L^2`

Where L is the length of the edge base. Calculating:

`\begin{gathered} A_b=\frac{\sqrt[]{3}}{4}\cdot6^2 \\ A_b=\frac{\sqrt[]{3}}{4}\cdot36 \\ A_b=9\text{ }\sqrt[]{3} \end{gathered}`

The lateral surface is:

Al = Base perimeter * Height

The base perimeter is the sum of its side lengths:

P = L + L + L = 18

Since the height is H = 10:

`\begin{gathered} A_l=18\cdot10 \\ A_l=180 \end{gathered}`

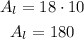
The total area is:

`\begin{gathered} S=2\cdot9\text{ }\sqrt[]{3}+180 \\ \boxed{S=18\text{ }\sqrt[]{3}+180} \end{gathered}`