Answer:
3/8
Explanation:
We want the probability of getting a tail in three trials.
We will use binomial distribution, given by the formula:

We want one success out of three trials. So, n = 3 and x = 1.
The probability for success in one trial is 1/2. So, p = 1/2.
And the probability for failure in one trial is 1/2. q = 1/2.
Therefore, the probability of getting a tail is:
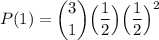
Evaluate:
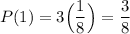
The probability of getting a tail by tossing a coin thrice is 3/8.
Edit:
My apologies. If you haven't learned the binomial distribution yet, below is another method.
Using the fundamental counting principle, we have a total of 2 times 2 times 2 or 8 total outcomes.
We want only one tail. This can be the first toss, the second toss, or the third toss.
So, out of 8 total outcomes, only 3 are favorable.
Hence, the probability of getting one tail by tossing a coin thrice is 3/8.