Answer:
(5, 8)
Explanation:
Since, the linear equation defined by
 and
and
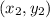 is,
is,
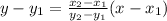
Thus, the linear equation defined by points (1, 6) and (3, 7) is,
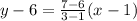
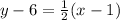
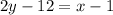
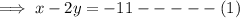
Similarly, the linear equation is defined by points (3, 6) and (5, 8),
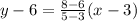
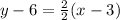
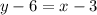
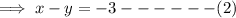
Equation (1) - equation (2),
-y = -8
⇒ y = 8
From equation (1),
x-2(8)=-11
x-16=-11
x = - 11 + 16 = 5
Hence, point (5,8) represents the solution of this system of equations.