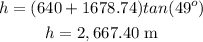Question

To estimate the height of a mountain, two students find the angle of elevation from a point (at ground level) b 640 meters from the base of the mountain to the top of the mountain is B = 49°. The students then walk a = 1950 meters straight back and measure the angle of elevation to now be a = 32°. If we assume that the ground is level, use this information to estimate the height of the mountain.

Answer 1

see the figure below to better understand the problem

step 1

In the right triangle ABC

we have that

`\begin{gathered} tan(32^o)=(h)/((640+1950+x)) \\ \\ h=(2590+x)tan(32^o)\text{ ----> equation 1} \end{gathered}`

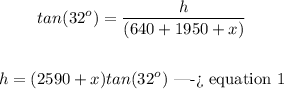
step 2

In the right triangle DBC

we have that

`\begin{gathered} tan(49^o)=(h)/((640+x)) \\ \\ h=(640+x)tan(49^o)\text{ ----> equation 2} \end{gathered}`

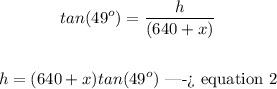
step 3

Equate equation 1 and equation 2 and solve for x

`\begin{gathered} (2590+x)tan(32^o)=(640+x)tan(49^o) \\ 2590tan32^o+xtan32^o=640tan49^o+xtan49^o \\ x[tan49^o-tan32^o]=2590tan32^o-640tan49^o \\ x=(2590tan32^o-640tan49)/([tan49^o-tan32^o]) \end{gathered}`

The value of x is equal to

x=1,678.74 meters

Find out the value of h

`\begin{gathered} h=(640+1678.74)tan(49^o) \\ h=2,667.40\text{ m} \end{gathered}`