Answer:
Using tangent ratio:
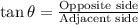
As per the statement:
a surveyor measures the angle of elevation to a point on a mountain to be 18.
⇒
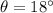
It is also given that the point on the mountain is horizontally 4 miles away from the surveyor.
⇒Adjacent side = 4 miles
You can see the diagram as shown below:
Using tangent ratio we have;
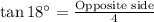
Multiply both sides by 4 we have;
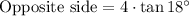
then;
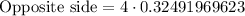
Simplify:
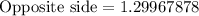
Therefore, the vertical change in elevation from the point where the surveyor is standing to the point on the mountain to the nearest hundredths is 1.30 miles