Answer: The correct option is (D)
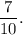
Step-by-step explanation: We are given to find the probability that a point chosen at random from segment AK is on segment CJ shown in the figure.
From the figure, we note that
the length of the line segment AK = 10 - 0 = 10,
and
the length of the line segment CJ = 9 - 2 = 7.
Let, 'T' denotes the event that a point chosen at random from the line segment AK lies on the line segment CJ.
So, n(T) = 7.
If 'S' denotes the sample space for the experiment, then
n(S) = 10.
Therefore, the probability that a point chosen at random from segment AK is on segment CJ is given by

Thus, the required probability is
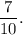
Option (D) is correct.