Question

Ellen wishes to mix candyworth a dollar and 45 cents per pound with candy worth $3.74 per pound to form 27 lb of a mixture worth $3.06 per pound how many pounds of the more expensive candy should she use

Answer 1

Ellen wishes to mix candy worth $1.45 per pound with candy worth $3.74 per pound to form 27 pounds of a mixture worth $3.06 per pound.

Let x be pounds of candy worth $1.45 per pound

Then we can set up the following equation

`1.45x+3.74(27-x)=3.06\cdot27`

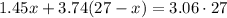
Where (27 - x) represents the pounds of candy worth $3.74 per pound

Let us solve this equation for x

`\begin{gathered} 1.45x+3.74(27-x)=3.06\cdot27 \\ 1.45x+100.98-3.74x=82.62 \\ 1.45x-3.74x=82.62-100.98 \\ -2.29x=-18.36 \\ 2.29x=18.36 \\ x=(18.36)/(2.29) \\ x=8.02\: lb\: \end{gathered}`

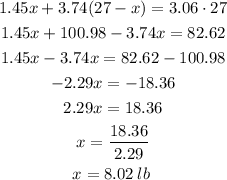
So, 8.02 pounds of less candy is required.

Whereas the pounds of more expensive candy will be

`27-x=27-8.02=18.98\: lb`

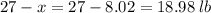
Therefore, 18.98 pounds of the more expensive candy should be used.