Question

Suppose you invest $50 a month in an annuity that earns 4.8% APR compounded monthly. how much money will you have in this account after 10 years?

Answer 1

`\bf \qquad \qquad \textit{Future Value of an ordinary annuity} \\\\ A=d\left[ \cfrac{\left( 1+(r)/(n) \right)^(nt)-1}{(r)/(n)} \right] \\\\\\ \qquad \begin{cases} A= \begin{array}{llll} \textit{compounded amount} \end{array} \begin{array}{llll} \end{array}\\ d=\textit{periodic deposits}\to &50\\ r=rate\to 4.8\%\to (4.8)/(100)\to &0.048\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{monthly, thus 12} \end{array}\to &12\\ t=years\to &10 \end{cases}`

Answer 2

$80.73.

Explanation:

We have been given that you invest $50 a month in an annuity that earns 4.8% APR compounded monthly. We are asked to find the amount of money in account after 10 years.

We will compound interest formula to solve our given problem.

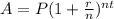`A=P(1+(r)/(n))^(nt)`, where,

A = Amount after t years,

P = Principal amount,

r = Interest rate in decimal form,

n = Number of times interest is compounded per year,

t = Time in years.

Let us convert our given interest rate in decimal form.

`4.8\%=(4.8)/(100)=0.048`

Upon substituting our given values in above formula we will get,

`A=\$50(1+(0.048)/(12))^(12*10)`

`A=\$50(1+0.004)^(120)`

`A=\$50(1.004)^(120)`

`A=\$50*1.6145278360416045`

`A=\$80.726391\approx \$80.73`

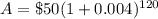
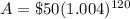
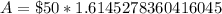
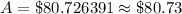
Therefore, we will have $80.73 in the account after 10 years.