Question

Peter is Landscaping a neighbor's circular flower garden he has one last election of the garden the needs to be filled the radius of the circle is 12 ft in the degrees is 85 degrees how many feet of stone will Peter need to fill this section of the garden

Answer 1

We can draw a picture so we have an idea on what the question is asking.

The question tells us that the circular region that is missing has a 85° degree and that the radius of the circle is 12 ft. Then, to solve the problem we need to calculate the area of the region. We can do it using the formula

`A=r\cdot(\theta)/(2)`

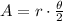
where r is the radius of the region and theta is the angle of the region in radians.

In here we have r=12 and we also have the measure of the angle is degrees. So we need to transform the angle to radians. REcall that to transform and angle from degrees to radians, we should multiply it by pi and then divide id by 180°. Lets calculate the angle in radians in our case

`\theta_{\text{rad}}=85\cdot(\pi)/(180)=\text{ 17}\cdot(\pi)/(36)`

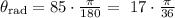
Then the area of the circular region is

`A=12\cdot(17\cdot\pi)/(36)\cdot(1)/(2)=17\cdot(\pi)/(6)`

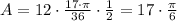
This is aproximately 8.901 square feet (taking an approximation of pi of 3.14159264)