Let's say you want to compute the probability
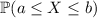
where

converges in distribution to

, and

follows a normal distribution. The normal approximation (without the continuity correction) basically involves choosing

such that its mean and variance are the same as those for

.
Example: If

is binomially distributed with
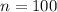
and
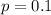
, then

has mean
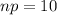
and variance

. So you can approximate a probability in terms of

with a probability in terms of

:
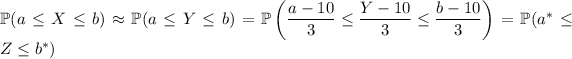
where
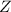
follows the standard normal distribution.