Answer:
D = -4/7 = - 0.57
C = 17/7 = 2.43
Step-by-step explanation:
We have the following two equations:
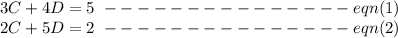
First, we isolate C from equation (2):

using this value of C from equation (3) in equation (1):
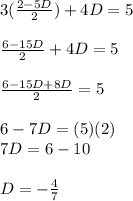
D = - 0.57
Put this value in equation (3), we get:
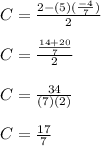
C = 2.43