Question

What rule can be used to find the next term of the arithmetic sequenc39, 60, 81, 102, 123, ...Oan = an-1-39Oan = an-1-21Oan = an-1 + 21Oan = an-1 + 39DONEThe next term of the arithmetic sequence39, 60, 81, 102, 123, ... isDONE

Answer 1

The answer for the first part is C.

The answer for the second part is 144.

Explanation:

Answer 2

Explanation

We are given the following arithmetic sequence:

`39,60,81,102,123,...`

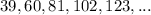
We are required to determine the rule to find the next term of the sequence.

We know that an arithmetic sequence goes from one term to the next by always adding (or subtracting) the same value. The number added (or subtracted) at each stage of the arithmetic sequence is called the common difference.

The common difference can be gotten as:

`\begin{gathered} Common\text{ }difference(d)=a_n-a_(n-1) \\ d=a_1-a_0=a_2-a_1 \\ \therefore d=60-39=81-60 \\ d=21 \\ \\ Substituting\text{ }the\text{ }value\text{ }into\text{ }the\text{ }initial\text{ }equation,\text{ }we\text{ }have \\ d=a_n-a_(n-1) \\ 21=a_n-a_(n-1) \\ Rearranging \\ 21+a_(n-1)=a_n \\ \therefore a_n=a_(n-1)+21 \end{gathered}`

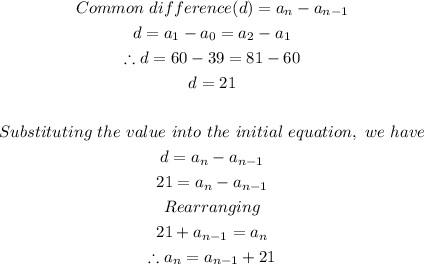
Hence, the answer is:

`a_n=a_(n-1)+21`

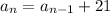
The third option is correct.

The next term of the sequence is: 123 + 21 = 144.