Answer:
Step-by-step explanation:
Given:
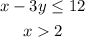
To find:
The graph of the inequalities and indicating the solution set of the system with crosshatching or shading
Recall that the slope-intercept form of the equation of a line is generally given as;
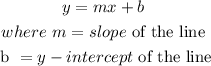
Let's rewritethe first inequality yin slope-intercept form using as seen below;
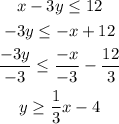
We can see from theabove that the slope (m)of the line is 1/3 and the y-intercept isi -4.
Since the inequality has a greater than sign, we'll shade the region above the line.
Also since the inqua;lity has an equal sign, the line will be solid.
See below the graph of the inequality;
For the second inequality, the line will be dashed since it does not have an equal sign. We'll shade the region to the right of the line since it has a greater than sign.
See below the graph of the inequality;
We will now go ahead and combine the two graphs, where thetwo shaded regions intersec isrepresent the solution set of the system as seen below;