Keywords:
equation, operations, equivalent, binomial, square root
For this case we have an equation in which we must apply operations to rewrite it in an equivalent way. We must start by raising both sides of the equation to the square. Thus, we eliminate the square root of the left side of equality and finally solve the binomial of the right side of equality.
So we have:
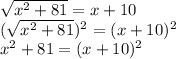
By definition:
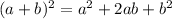
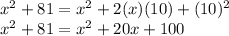
Thus,
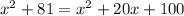 is equivalent to
is equivalent to
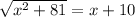
Answer:
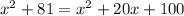
Option D