Question

What is the horizontal asymptote of the function f(x)= (x-2)over(x-3)^2

a. y = 0
b. y = 1
c. y = 2
d. y = 3

Answer 1

the answer is a
there's not a horizontal asymptote
y = 0

Answer 2

A.
`y=0`

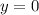
Explanation:

We have been given a function
`f(x)=(x-2)/((x-3)^2)` and we are asked to find the horizontal asymptote of our given function.

Let us recall the rules for a horizontal asymptote.

• If polynomials of denominator and numerator of a rational function have same degree, then horizontal asymptote will be the quotient of coefficients of the highest degree terms.
• If the polynomial of denominator has larger degree than the numerator, then the horizontal asymptote will be the x-axis or
  `y=0`.
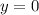• If the polynomial of numerator has larger degree than denominator, then the function has no horizontal asymptote.

First of all let us expand the square given for the denominator.

`f(x)=(x-2)/(x^2-6x+9)`

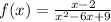
Now we can see that denominator of our triangle is a second degree polynomial, while numerator is a 1st degree polynomial.

Since denominator has larger degree than numerator, therefore, our function will have a horizontal asymptote at
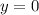`y=0` and option A is the correct choice.