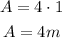ANSWER and EXPLANATION
To plot the velocity at different times, we have to find the slope of the graph at those times.
So, we find the slope between 0 - 1, 0 - 2, 0 - 3, and 0 - 4 seconds using the formula:
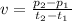
Therefore, we have that the velocity at the time intervals is as follows:

As we can see, the velocity is constant throughout the motion.
Now, we have to plot this information on the velocity-time graph
To find the displacement from the graph, we have to find the area of the rectangle that has the vertices (0, 0), (4, 0), (4, 1), and (0, 1).
The area of a rectangle is given as:

where L = length, W = width
The length of the rectangle is the horizontal distance between (4, 0) and (0, 0) which is 4 and the width is the vertical distance between (0, 1) and (0, 0) which is 1.
Therefore, the displacement (area under the graph) is: