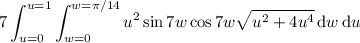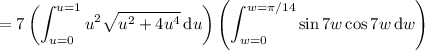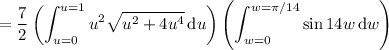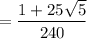Question

Evaluate the surface integral. ??s yz ds s is the surface with parametric equations x = u2, y = usin(7w, z = ucos(7w, 0 ? u ? 1, 0 ? w ? ?/(14.

Answer 1

Taking a wild guess on what the question says...

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =


`\displaystyle\iint_Syz\,\mathrm ds`

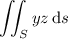
where
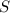
`S` is the surface parameterized by


`\mathbf r(u,w)=\mathbf r(x(u,w),y(u,w),z(u,w))=\left\langle u^2,u\sin7w,u\cos7w\right\rangle`

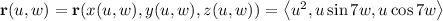
for
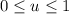
`0\le u\le1` and
`0\le w\le\frac\pi{14}`.

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

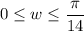
The surface integral is equivalent to


`\displaystyle\iint_S y(u,w)z(u,w)\left\|\mathbf r_u*\mathbf r_w\right\|\,\mathrm du\,\mathrm dw`

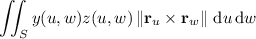
where you have


`\mathbf r_u=\left\langle2u,\sin7w,\cos7w\right\rangle`

`\mathbf r_w=\left\langle0,7u\cos7w,-7u\sin7w\right\rangle`

`\implies\mathbf r_u*\mathbf r_w=\left\langle-7u,14u^2\sin7w,14u^2\cos7w\right\rangle`

`\implies\left\|\mathbf r_u*\mathbf r_w\right\|=7√(u^2+4u^4)`

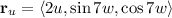
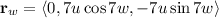
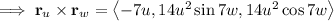
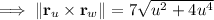
The integral then becomes


`\displaystyle7\int_(u=0)^(u=1)\int_(w=0)^(w=\pi/14)u^2\sin7w\cos7w√(u^2+4u^4)\,\mathrm dw\,\mathrm du`

`=\displaystyle7\left(\int_(u=0)^(u=1)u^2√(u^2+4u^4)\,\mathrm du\right)\left(\int_(w=0)^(w=\pi/14)\sin7w\cos7w\,\mathrm dw\right)`

`=\displaystyle\frac72\left(\int_(u=0)^(u=1)u^2√(u^2+4u^4)\,\mathrm du\right)\left(\int_(w=0)^(w=\pi/14)\sin14w\,\mathrm dw\right)`

`=(1+25\sqrt5)/(240)`