Question

Vern sold his 1964 Ford Mustang for $55,000 and wants to invest the money to earn him 5.2% interest per year. He will put some of the money into Fund A that earns 4% per year and the rest in Fund B that earns 10% per year. How much should he invest into each fund (in dollars) if he wants to earn 5.2% interest per year on the total amount

Answer 1

Let x = the amount in fund A.

Let y = the amount in fund B.

Interest fund A = 4% = 0.04

Interest fund B = 10% = 0.10

Then, according to the information given we have that:

x + y = 55000

And the formula for determining simple interest is given by:

`I=PRT`

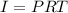
Where:

P = initial capital

R = interest rate

T = time

We have the following equation

`\begin{gathered} 0.04x+0.10y=0.052(55000) \\ 0.04x+0.10y=2860 \end{gathered}`

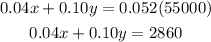
Next, we solve the system of two equations.

From the first equation we clear x:

`\begin{gathered} x+y=55000 \\ x+y-y=55000-y \\ x=55000-y \end{gathered}`

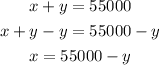
Substitute x in the second equation:

`\begin{gathered} 0.04x+0.10y=2860 \\ 0.04(55000-y)+0.10y=2860 \end{gathered}`

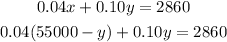
Simplify

`\begin{gathered} 2200-0.04y+0.10y=2860 \\ 2200+0.06y=2860 \end{gathered}`

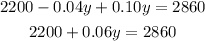
Solve for y:

`\begin{gathered} 2200+0.06y-2200=2860-2200 \\ 0.06y=660 \\ (0.06y)/(0.06)=(660)/(0.06) \\ y=11000 \end{gathered}`

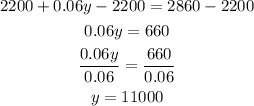
Then, for x:

`x=55000-y=55000-11000=44000`

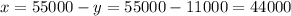
Answer:

Fund A = $44000

Fund B = $11000