Question

For which of the following angles is cosecant undefined? 45° 60° 180° 270°

Answer 1

Cosecant = 1/sin so it is where sin =0. Out of these sin is 0 at 180 degrees

Answer 2

Answer: Cosecant is undefined at 180°.

Explanation:

Since we have given that

Cosecant i.e. cosec Θ

Since we know from the "trigonometric table"

If Θ = 45°

`cosec\ 45^\circ=√(2)`

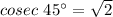
so, cosecant is defined.

If Θ = 60°,

`cosec\ \theta=(2)/(√(3))`

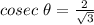
So, cosecant is defined again.

If Θ = 180°

`cosec\ (180^\circ)=-cosec\ 0^\circ=\infty`

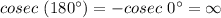
So, it is not defined.

If Θ = 270°

then
`cosec\ 270^\circ=(-)cosec\ 90^\circ=-1`

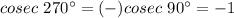
so, it is defined.

Hence, cosecant is undefined at 180°.