Answer:
40 feet.
Explanation:
Area of rectangle = 800 square feet
Let the fourth side of the rectangle be x.
Length of the rectangle = x feet
The area of a rectangle is
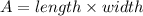
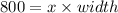
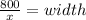
Cost of fencing = $5 per foot
Cost function on three sides is
![C(x)=5[length+2(width)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/avpfig4phm3qll97f2t3yfmwryqzq86543.png)
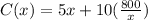
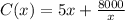
Differentiate with respect to x.
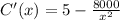
![[\because (d)/(dx)((1)/(x))=-(1)/(x^2)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/iedzdyg7u85t1zvt3uu81n0mcl49tefli1.png)
To find the critical point equate C'(x)=0.
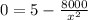
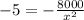
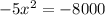
Divide both sides by -5.
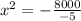

Taking square root on both sides,
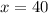
Differentiate C'(x) with respect to x.

Since C''(x)>0 for x=40, therefore cost of the fencing is minimum at x=40.
Thus, the measure of fourth side of the rectangle is 40 feet.