We need to simplify
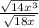
First lets factor


=
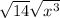

by applying the radical rule
![\sqrt[n]{ab} = \sqrt[n]{a} \sqrt[n]{b}](https://img.qammunity.org/2018/formulas/mathematics/high-school/4wgenh2d0e0l14390hbj80h71flx9d7iqa.png)
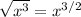
By applying the radical rule
![\sqrt[n]{x^m} = x^(m/n)](https://img.qammunity.org/2018/formulas/mathematics/high-school/8e2yufn379arzxg5pv7bg6m33poe9cf4nh.png)
So

=
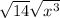
=
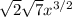
Now let's factor
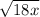
By applying the radical rule
![\sqrt[n]{ab} = \sqrt[n]{a} \sqrt[n]{b}](https://img.qammunity.org/2018/formulas/mathematics/high-school/4wgenh2d0e0l14390hbj80h71flx9d7iqa.png)
,
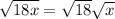
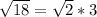
So
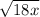
=
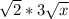
So
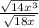
=
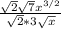
We know that
![\sqrt[n]{x} = x^(1/n)](https://img.qammunity.org/2018/formulas/mathematics/high-school/8dy8gektpj45agp5biomwt4sb60d8pwa6c.png)
so
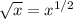
We now have
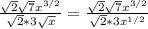
We know that
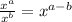
So
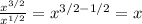
We now got
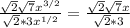
We can notice that the numerator and the denominator both got √2 in a multiplication, so we can simplify them, and we get:
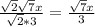
All in All, we get
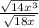
=
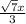
Hope this helps! :D