Question

A population of 120,000 grows 4% per year after 16 years. How much will the population be after 16 years?

Answer 1

Let's consider the scenario after each year:

After the zeroth year, the population is: 120 000(1 + 0.04)⁰
After the first year, the population is: 120 000(1 + 0.04)¹
After the second year, the population is: 120 000(1 + 0.04)²
...

Thus, we can find the general rule:
After the nth year, the population is: 120 000(1 + 0.04)ⁿ
And after the 16th year, the population is 120 000(1 + 0.04)¹⁶ = 224 758 (rounded to nearest whole number)

Answer 2

The population after 16 years will be: 224758 people

How too solve the exponential model?

The general form of an exponential equation is:

y = a(b)ˣ

where:

a is any nonzero number,

b is a positive real number not equal to 1.

x is the input variable that occurs as an exponent

We are given:

a = 120000

b = 4% = 1.04

Thus, the equation is:

y = 120000
`(1.04)^(x)`

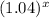
After 16 years, we have:

y = 120000
`(1.04)^(16)`

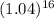
y = 224758 people