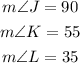In a right triangle, the acute angles are complementary angles, which means that their measures add up to 180º. Then:
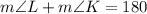
Replace the expressions for the measure of L and K in terms of x. Then, solve for x and substitute its value back into the expressions for L and K to find their values. Since angle J is a right angle, its measure is 90º.
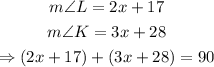
Solve for x:
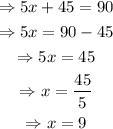
Replace x=9into the expressions for L and K:
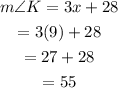
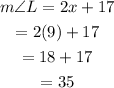
Therefore, the measures of the angles are: