Question

Can someone verify that the answer is A? 

Line H is represented by the following equation: 2x + 2y = 8

What is most likely the equation for line K so the set of equations has infinitely many solutions?

A x + 2y = 2
B x + y = 4
C 2x + y = 6
D x − y = 8

Answer 1

The answer is A because:...
2x + 2y = 8
You need to simplify it by getting either the x or the y by itself so you need to divide everything by two.
= x + y = 4
I hope this helped!!:)

Answer 2

Option: B is the correct answer.

B. x+y=4

Explanation:

The equation of the line H is given by:

`2x+2y=8`

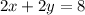
i.e. on dividing both the side of the equation by 2 we get:

`x+y=4--------(1)`

Now, in order for a system to have infinite many solution the two lines must intersect infinite times.

A)

`x+2y=2`

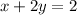
Now, when we subtract equation(1) from this equation we have:

`y=-2`

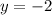
and

`x=6`

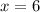
i.e. the solution is : (6,-2)

i.e. the system has a unique solution.

B)

`x+y=4`

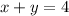
This equation is similar to equation (1).

Hence, the system has infinite many solution.

C)

`2x+y=6`

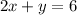
When, we subtract equation (1) from this equation we have:

`x=2`

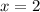
and

`y=2`

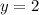
Hence, the system has a unique solution.

D)

`x-y=8`

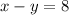
On adding this equation to equation (1) we get:

`2x=12\\\\i.e.\\\\x=6`

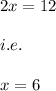
and

`y=-2`

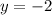
Hence, the solution is unique i.e. (6,-2)