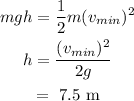Given:
The mass of the cart is m = 100 kg
The radius of the track is r = 15 m
To find
(a) Minimum speed required to reach the top of the loop
(b) The height of the hill
Step-by-step explanation:
(a) The formula to calculate minimum speed is
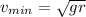
Here, g = 9.8 m/s^2 is the acceleration due to gravity.
On substituting the values, the minimum speed will be
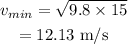
(b) The height of the hill required to make it through the loop is