Question

Prove that among any 54 integers 1 =< x1 < x2 < x3 <...< x54 =< 100, there is a pair with difference 12.

Answer 1

Use the pigeonhole principle.

Consider choosing


`x_i=\begin{cases}i&\text{for }i\in\{1,2,\ldots,12\}\\24-(12-i)=12+i&\text{for }i\in\{13,14,\ldots,24\}\\36-(12-i)=24+i&\text{for }i\in\{25,26,\ldots,36\}\\48-(12-i)=36+i&\text{for }i\in\{37,38,\ldots,48\}\\60-(12-i)=48+i&\text{for }i\in\{49,50,51,52,53,54\}\end{cases}`

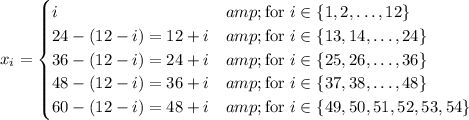
This selection guarantees that no two elements have a difference of 12. For example, in the first subset with
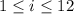
`1\le i\le12`, the largest difference is 12 - 1 = 11. Then in the next subset with
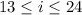
`13\le i\le24`, the smallest difference between the least element of this subset with the previous subset is 25 - 12 = 13.

The last subset is problematic, however, because the last two elements of that subset are 48 + 53 = 101 and 48 + 54 = 102. We require that all the integers are no greater than 100, and that they are distinct, which means there must be two numbers
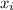
`x_i` that belong to the set
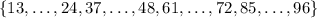
`\{13,\ldots,24,37,\ldots,48,61,\ldots,72,85,\ldots,96\}`, and this will force at least one integer that makes up a pair with difference 12.