We have the system of equations:
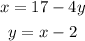
We already have an explicit expression both for x and y so we can use any of the two equations and replace the variable in the other one.
We will substitute y in the first equation, with the information of the second equation, and solve for x:

Then, we can use the value of x to calculate y with the second equation:
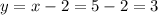
We can check the result by replacing the solution values in the equation and verify that we get a valid result:
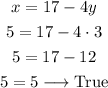
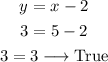
Answer: the solution is x=5 and y=3