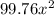Answer:
Area of the rectangle(A) is given by:
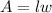
where,
l is the length and w is the width of the rectangle respectively.
As per the statement:
The yard is rectangular and measures 10x by 15x
⇒
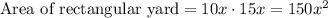
It is also given that:
the fountain is going to be circular with a radius of 4x.
Area of a circle(A') is given by:
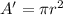 where, r is the radius of the circle.
where, r is the radius of the circle.
Use

then;
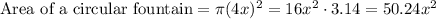
We have to find the he area of the remaining yard.

Substitute the given values we have;
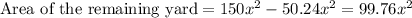
Therefore, the area of the remaining yard will be,