Question

Describe the effect an increase in i, the interest rate applied to the present value, has on the monthly payment P in the formula a. An increase in i, the interest rate, will not change P, the monthly payment. b. An increase in i, the interest rate, will create an increase in P, the monthly payment. c. An increase in i, the interest rate, will create a decrease in P, the monthly payment. d. An increase in i, the interest rate, can increase or decrease P, the monthly payment, depending on the value of PV.

Answer 1

Option B is the correct answer - An increase in i, the interest rate, will create an increase in P, the monthly payment.

Explanation:

The monthly payment formula is

`p=(r(PV))/(1-(1+r)^(-n) )`

where p = monthly payment, r = rate of interest, n = time period and PV = present value.

Here 'r' is proportional to p. When r increases, p increases and vice versa.

Hence, option B is correct.

Summing up in simple language, we always see, when the rate of interest is higher, the installments are higher and when rate is lower the monthly installments are less.

Answer 2

B. An increase in i, the interest rate, will create an increase in P, the monthly payment.

Explanation:

We have the formula for the monthly payment as,

`P=(i * PV)/(1-(1+i)^(-n) )`,

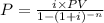where P = monthly payment, i = rate of interest, PV = present value and n = time period.

Now, as i increase we get that (1+i) increases and so
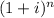`(1+i)^(n)` increases.

This gives us that,
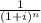`(1)/((1+i)^(n) )` decreases and so
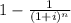`1-(1)/((1+i)^(n))` decreases

Therefore,
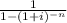`(1)/(1-(1+i)^(-n) )` increases.

So, we get that as i increases , the value of P will increase.

Hence, option B is correct.