Question

What value represents the horizontal translation from the graph of the parent function f(x) = x2 to the graph of the function g(x) = (x – 4)2 + 2?

Answer 1

to move a function c units to the right, minus c from every x

we got

fro x^2 to (x-4)^2+2
4 was minused from every x
it was moved 4 units to the right

Answer 2

The value of horizontal shift is
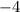`-4` that means graph of parent function is shifted to right by 4 units.

Step-by-step explanation:

We have been given a parent function
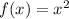`f(x)=x^2` and another function
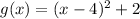`g(x)=(x-4)^2+2`. We are asked to determine the horizontal translation from the graph of the parent function to the graph of the function g(x).

Let us recall translation rules.

Horizontal translation:

`f(x)\rightarrow f(x-a)=\text{Graph shifted to the right by 'a' units}`

`f(x)\rightarrow f(x+a)=\text{Graph shifted to the left by 'a' units}`

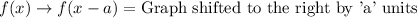
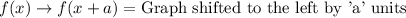
Vertical translation:

`f(x)\rightarrow f(x)-a=\text{Graph shifted downwards by 'a' units}`

`f(x)\rightarrow f(x)+a=\text{Graph shifted upwards by 'a' units}`

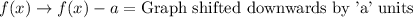
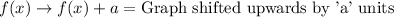
Upon looking at our both functions, we can see that parent function is shifted to right by 4 units and upwards by 2 units to get the the function g(x).

Therefore, the value of horizontal translation is
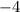`-4`, which indicates the graph is shifted to right by 4 units.