Question

Use the rational zeros theorem for all possible rational zeros

Answer 1

The Rational Zeros Theorem predicts possible rational zeros of a polynomial function by creating a list of ratios from factors of the constant term and the leading coefficient. Synthetic division helps to test these zeros. Checking the answer and considering the significance of numbers in scientific notation are important steps in the process.

Step-by-step explanation:

Understanding the Rational Zeros Theorem

The Rational Zeros Theorem is used in algebra to predict the possible rational zeros of a polynomial function. Given a polynomial function with integer coefficients, the possible rational zeros are the ratios (positive and negative) of the factors of the constant term to the factors of the leading coefficient. When using this theorem, it's important to eliminate terms to simplify the algebra.

To apply the theorem, you would list all possible rational zeros and then use synthetic division or the polynomial remainder theorem to test whether these candidates are indeed zeros of the polynomial. If any of the listed possible rational zeros yields a remainder of zero, it is a zero of the polynomial. It is also important to check the answer to ensure it is reasonable, which often involves further verification or evaluation of the polynomial at the found zeros.

In addition to calculating possible rational zeros, it is important to understand the significance of digits in reported numbers. In scientific notation, for instance, all numbers reported before the multiplication sign, including zeros, are significant and contribute to the precision of the reported measurement.

Answer 2

The rational zero theorem states that if the polynomial has integer coefficients, then every rational zeros of the function has the form p/q, where p is a factor of the constant term and q is a factor of the leading coefficient.

Considering the polynomial

`f(x)=2x^3+5x^2+5x+3`

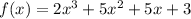
The leading coefficient is the coefficient of the first term, which is 2

The factors are q ±1, ±2

The constant of the polynomial is 3

The factors are p: ±1, ±3

Next, determine all possible values of p/q

First, for p= ±1 and q=±1,±2

`\begin{gathered} (p)/(q)=(\pm1)/(\pm1)=\pm1 \\ (p)/(q)=(\pm1)/(\pm2)=\pm(1)/(2) \end{gathered}`

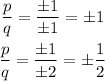
Second, for p=±3 and q=±1, ±2

`\begin{gathered} (p)/(q)=(\pm3)/(\pm1)=\pm3 \\ (p)/(q)=(\pm3)/(\pm2)=\pm(3)/(2) \end{gathered}`

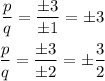
The possible rational zeros of the polynomial are ±1, ±1/2, ±3/2, and ±3