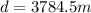Question

A 4 g bullet is fired horizontally with a speed of 300m/s into 0.8 kg block of wood at rest on a table. If the coefficient of friction between block and table is 0.3, how far will the block slide approximately?

Answer 1

momentum:
p₁ = m₁v₁
p₂ = m₂v₂

p₃ = (m₁+ m₂) v

p₁ + p₂ = p₃

v = p₁ + p₂ / (m₁ + m₂)

friction:
F = μ(m₁ + m₂)g = (m₁ + m₂)a ⇒ a = μg

equations of motion:
v = at = μgt ⇒ t = v/μg
x = 1/2 at² = 1/2 μg * v²/(μg)² = 1/2 v² / μg

v₁ = 300 m/s
v₂ = 0 m/s
m₁ = 0.004 kg
m₂ = 0.8 kg
μ = 0.3
g = 9.81 m/s²

x = displacement

Answer 2

d = 3784.5 m

Step-by-step explanation:

First bullet goes into the block and fixed into it

so here the speed of the combined is given by momentum conservation

so it is given as

`mv_o = (m + M) v`

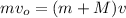
here we know that

`m = 4 g = 0.004 kg`

`M = 0.8 kg`

`v_o = 300 m/s`

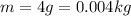
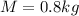
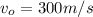
now from above formula

`(0.004)(300) = (0.004 + 0.8) v`

`v = 149.25 m/s`

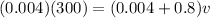
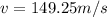
now the coefficient of friction on the floor is given as

`\mu = 0.3`

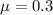
so the deceleration is given as

`a = -\mu g`

`a = -(0.3)9.81`

`a = -2.943 m/s^2`

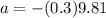
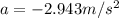
now from equation of kinematics we know that

`v_f^2 - v_i^2 = 2 a d`

`0 - 149.25^2 = 2(-2.943)d`

`d = 3784.5 m`