Question

It takes 8 minutes for Byron to fill the kiddie pool in the backyard using only a handheld hose. When his younger sister is impatient, Byron also uses the lawn sprinkler to add water to the pool so it is filled more quickly. If the hose and sprinkler are used together, it takes 5 minutes to fill the pool. Which equation can be used to determine r, the rate in parts per minute, at which the lawn sprinkler would fill the pool if used alone?

Answer 1

Since you know that the hose will fill the whole pool in 8 minutes you know it will fill 1/8 of the pool per minute. In 5 minutes it will fill up 5/8 of the pool. This will make your equation 5/8 +5r=1. Solving for r will give you 3 parts/40 minutes

Answer 2

Rate at which sprinkler will fill the pool is
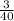`(3)/(40)` per minute.

Explanation:

It takes 8 minutes for Byron to fill the kiddie pool in the backyard with the use of handheld hose only.

So part of kiddie pool filled in one minute =
`(1)/(8)`

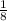
When lawn sprinkler and handheld hose both were used to fill the pool,it took 5 minute to fill the pool together.

Now the part of pool filled in one minute =
`(1)/(5)`

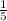
If the sprinkler fills the pool alone in r minutes then the pool filled per minute will be =
`(1)/(r)`

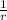
Now we combine these three facts to form the equation.

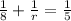
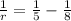
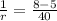
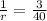
`(1)/(8)+(1)/(r)=(1)/(5)`

`(1)/(r)=(1)/(5)-(1)/(8)`

`(1)/(r)=(8-5)/(40)`

`(1)/(r)=(3)/(40)`

r =
`(40)/(3)`

Therefore, time taken by sprinkler alone will be 13.33 minutes and the rate per minute at which sprinkler will fill the pool is
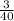`(3)/(40)`.