Answer:
The vertex form of each function is
 ,
,
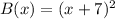 ,
,
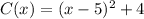 and
and
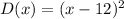 .
.
Explanation:
The given function is
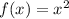
The vertex form of a parabola is

Where, (h,k) is vertex.
If is given that the functions A(x), B(x), C(x) and D(x) are transformed by f(x). So, the value of a is 1 for each function.
The graph of A(x) shifts 8 units down and the vertex of the parabola is (0,-8). Therefore the vertex form of A(x) is
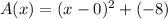

The graph of B(x) shifts 7 units left and the vertex of the parabola is (-7,0). Therefore the vertex form of B(x) is

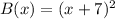
The graph of C(x) shifts 5 units right and 4 units up and the vertex of the parabola is (5,4). Therefore the vertex form of C(x) is
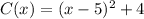
The graph of D(x) shifts 12 units right and the vertex of the parabola is (12,0). Therefore the vertex form of D(x) is

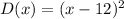
Therefore the vertex form of each function is
 ,
,
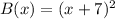 ,
,
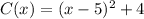 and
and
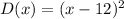 .
.