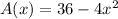Question

A square is 6 inches on each side. A small square, x inches on each side, is cut out from each corner of the original square. Represent the area of the remaining portion of the square in the form of a polynomial function A(x)

.

Answer 1

Draw a square with 4 equal sides that are 6 inches long. Then draw a small square on a corner of your drawn square. A(x) = 36 - A^2

a being the area of the smaller square
A^2= area of a square.

Answer 2

`A(x) = 36-4x^2`

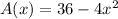
Explanation:

Side of original Square = 6 inches

Area of square =
`Side^2`

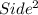
Area of square =
`6^2`

=
`36 inches^2`

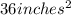
Now we are given that A small square, x inches on each side, is cut out from each corner of the original square

Area of small square =
`Side^2 = x^2`

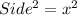
Original square has four corners

So, Area 4 small squares =
`4x^2`

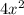
Let the remaining area be A(x)

So, Remaining area = Original Area - Area of 4 small squares

`\Rightarrow A(x) = 36-4x^2`

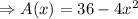
Hence the area of the remaining portion of the square in the form of a polynomial function A(x) is
`A(x) = 36-4x^2`