Let
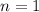
. Then
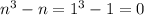
. By convention, every non-zero integer

divides 0, so
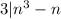
.
Suppose this relation holds for
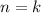
, i.e.
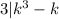
. We then hope to show it must also hold for
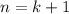
.
You have

We assumed that
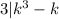
, and it's clear that

because
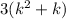
is a multiple of 3. This means the remainder upon divides
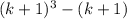
must be 0, and therefore the relation holds for
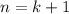
. This proves the statement.