In case of a moderately skewed distribution, the difference between mean and mode is almost equal to three times the difference between the mean and median.
![\operatorname{mean}-mode=3(\operatorname{mean}-\operatorname{median})]()
Using this rule in our problem, we have
![\begin{gathered} 155.89-154=3(155.89-\operatorname{median}) \\ 1.89=3(155.89-\operatorname{median}) \\ 0.63=155.89-\operatorname{median} \\ \operatorname{median}=155.89-0.63 \\ \operatorname{median}=155.26 \end{gathered}]()
The median is $155.26.
If a frequency distribution graph has a symmetrical frequency curve, then mean, median and mode will be equal.
In case of a positively skewed frequency distribution, the mean is always greater than median and the median is always greater than the mode.
In case of a negatively skewed frequency distribution, the mean is always lesser than median and the median is always lesser than the mode.
In our problem, the mean is greater than the median
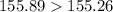
and the median is greater than the mode

Therefore, we have a positively skewed frequency distribution.